SLEEPY Benchmark#
The following notebook is for comparing SLEEPY performance among different systems. We run each simulation with and without parallel usage to determine additionally where parallel processing improves behavior. Plotting is not counted in computational time.
import SLEEPY as sl
from time import time
import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
import subprocess
import sys
Loading Defaults from file
Versions#
print(f'Python: {sys.version.split(" (")[0]}')
print(f'Numpy: {np.version.version}')
print(f'Scipy: {sp.version.version}')
try:
result = subprocess.run(['pip','show','multiprocess'], stdout=subprocess.PIPE)
vs=result.stdout.decode().split('Version: ')[1].split('Summary')[0].strip()
print(f'Multiprocess: {vs}')
except:
print('Multiprocess is not installed (recommended)')
if hasattr(np.__config__,'blas_mkl_info') and 'mkl_rt' in np.__config__.blas_mkl_info['libraries']:
print('Uses Intel MKL')
else:
print('Intel MKL not in use (recommended)')
Python: 3.11.13
Numpy: 1.24.3
Scipy: 1.10.1
Multiprocess: 0.70.15
Uses Intel MKL
Benchmark 1: \(R_{1\rho}\) relaxation#
sl.Defaults['cache']=True
for parallel in [False,True]:
sl.Defaults['parallel']=parallel
t0=time()
ex0=sl.ExpSys(600,Nucs=['15N','1H'],vr=60000,pwdavg=2,n_gamma=30)
ex0.set_inter('dipole',i0=0,i1=1,delta=22000)
ex0.set_inter('CSA',i=0,delta=110,euler=[0,15,0])
ex1=ex0.copy()
ex0.set_inter('dipole',i0=0,i1=1,delta=22000,euler=[0,30,0])
ex0.set_inter('CSA',i=0,delta=110,euler=[[0,15,0],[0,30,0]])
L=sl.Liouvillian(ex0,ex1,kex=sl.Tools.twoSite_kex(1e-6))
seq=L.Sequence().add_channel('15N',v1=35000)
rho=sl.Rho(rho0='15Nx',detect='15Nx')
rho,seq=rho.ReducedSetup(seq)
rho.DetProp(seq,n=1000)
print(f'{"Parallel" if parallel else "Series"} time: {(time()-t0)*1e3:.0f} ms')
print(f'Propagators calculated: {rho.L._PropCache.cache_count[0]}, Propagators from cache: {rho.L._PropCache.cache_count[1]}')
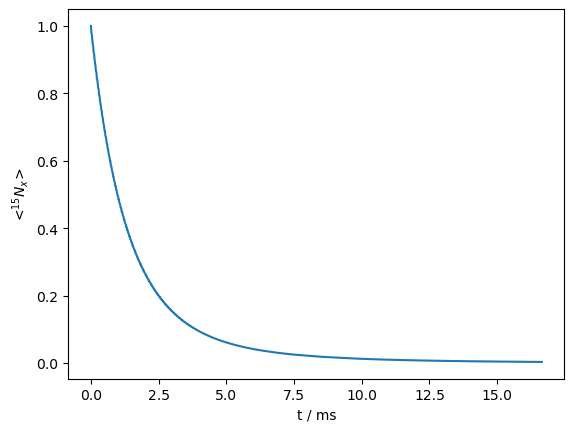
rho.plot()
State-space reduction: 32->16
Series time: 231 ms
Propagators calculated: 1470, Propagators from cache: 0
State-space reduction: 32->16
Parallel time: 267 ms
Propagators calculated: 1286, Propagators from cache: 0
<Axes: xlabel='t / ms', ylabel='<$^{15}N_x$>'>
Benchmark 2: REDOR#
sl.Defaults['cache']=True
for parallel in [False,True]:
sl.Defaults['parallel']=parallel
t0=time()
ex0=sl.ExpSys(v0H=600,Nucs=['15N','1H'],vr=60000,pwdavg=sl.PowderAvg('bcr20'),n_gamma=30)
# After varying the powder average and n_gamma
# a beta-average and 30 gamma angles were determined to be sufficient
delta=sl.Tools.dipole_coupling(.102,'15N','1H')
phi=35*np.pi/180
ex0.set_inter('dipole',i0=0,i1=1,delta=delta)
L=sl.Tools.Setup3siteSym(ex0,tc=1e-9,phi=phi)
v1=120e3 #100 kHz pulse
tp=1/v1/2 #pi/2 pulse length
t=[0,L.taur/2-tp,L.taur/2,L.taur-tp,L.taur]
first=L.Sequence().add_channel('1H',t=t,v1=[0,v1,0,v1],phase=[0,0,0,np.pi/2,0])
t=[0,tp,L.taur/2,L.taur/2+tp,L.taur]
second=L.Sequence().add_channel('1H',t=t,v1=[v1,0,v1,0],phase=[np.pi/2,0,0,0,0])
center=L.Sequence().add_channel('15N',t=[0,L.taur/2-tp/2,L.taur/2+tp/2,L.taur],
v1=[0,v1,0])
Ucenter=center.U()
Ufirst=first.U()
Usecond=second.U()
rho=sl.Rho('15Nx','15Nx')
U1=L.Ueye()
U2=L.Ueye()
for k in range(48):
rho.reset()
(U2*Ucenter*U1*rho)()
U1=Ufirst*U1
U2=Usecond*U2
print(f'{"Parallel" if parallel else "Series"} time: {(time()-t0):.1f} s')
print(f'Propagators calculated: {L._PropCache.cache_count[0]}, Propagators from cache: {L._PropCache.cache_count[1]}')
Series time: 18.4 s
Propagators calculated: 13800, Propagators from cache: 45000
Parallel time: 29.2 s
Propagators calculated: 13801, Propagators from cache: 43662
Above, we also evaluated how many propagators could be recycled. In parallel mode, propagator storage and propagator usage counts are asynchronously edits, so simultaneous edits to shared variables may affect the accuracy of the counts.
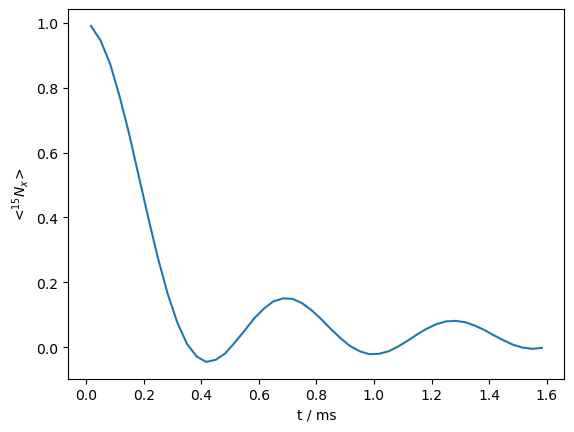
rho.plot()
<Axes: xlabel='t / ms', ylabel='<$^{15}N_x$>'>
Benchmark 3: Pseudocontact shift under MAS#
sl.Defaults['cache']=True
for parallel in [False,True]:
sl.Defaults['cache']=True
sl.Defaults['parallel']=parallel
t0=time()
delta=sl.Tools.dipole_coupling(1,'e-','13C') #10 Angstroms from electron
ex=sl.ExpSys(v0H=600,Nucs=['13C','e-'],vr=6000,LF=True,T_K=200,pwdavg=6,n_gamma=30) #Electron-nuclear system
ex.set_inter('hyperfine',i0=0,i1=1,Axx=-delta/2,Ayy=-delta/2,Azz=delta)
ex.set_inter('g',i=1,gxx=1,gyy=1,gzz=4)
L=sl.Liouvillian(ex) #Generate a Liouvillian
L.add_relax('T1',i=1,T1=2e-8,OS=True,Thermal=True)
L.add_relax('T2',i=1,T2=2e-8,OS=True)
seq=L.Sequence() #Generate an empty sequence
rho200=sl.Rho('13Cx','13Cp') #Generate initial state, detection operator
_=rho200.DetProp(seq,n=8000,n_per_seq=1) #Propagate the system
rho200.downmix()
print(f'{"Parallel" if parallel else "Series"} time: {(time()-t0):.1f} s')
print(f'Propagators calculated: {L._PropCache.cache_count[0]}, Propagators from cache: {L._PropCache.cache_count[1]}')
L._PropCache.cache_count[:]=0
t0=time()
rho200.clear().DetProp(seq,n=8000,n_per_seq=1).downmix()
print(f'{"Parallel" if parallel else "Series"} time after caching: {(time()-t0):.1f} s')
print(f'Propagators calculated: {L._PropCache.cache_count[0]}, Propagators from cache: {L._PropCache.cache_count[1]}')
Series time: 18.1 s
Propagators calculated: 8970, Propagators from cache: 0
Series time after caching: 1.8 s
Propagators calculated: 0, Propagators from cache: 8970
Parallel time: 17.8 s
Propagators calculated: 8970, Propagators from cache: 0
Parallel time after caching: 1.8 s
Propagators calculated: 0, Propagators from cache: 8970
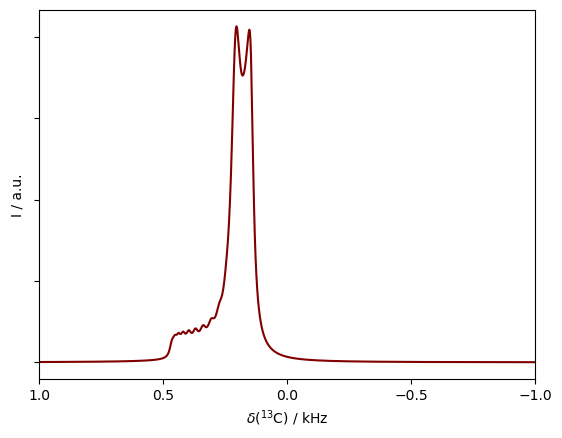
ax=rho200.plot(FT=True,color='maroon') #Plot the results into the same axis
ax.set_xlim([1,-.5])
ax.set_yticklabels('')
_=ax.set_xticks([-1,-.5,0,.5,1])
Benchmark 4: Water hopping (4/5/6-spin simulation)#
n=3 #Number of 1H (number of spins is n+1)
sl.Defaults['cache']=True
for parallel in [False,True]:
sl.Defaults['parallel']=parallel
t0=time()
# CH couplings
delta=np.array([4606.92351485, 1797.74007351, 3013.38969601, 1109.64922884,
2016.55071255, 985.46533497])
beta=np.array([1.52269289, 1.32442461, 1.72911212, 2.00710785, 0.79886871,
2.50129217])
gamma=np.array([ 0.90747836, 1.24462096, -1.94198315, -2.26840075, -0.28942014,
-0.97775707])
# HH couplings
deltaHH=np.array([[240240.30545617, 61146.36447292, 1970.3813349 ,
1155.61145146, 6094.10132617, 1985.91135194],
[ 61146.36447292, 240240.30545617, 1794.04721071,
1006.48333044, 5846.61932559, 2152.90241365],
[ 1970.3813349 , 1794.04721071, 240240.30545617,
61145.15653655, 2294.80686596, 7166.863992 ],
[ 1155.61145146, 1006.48333044, 61145.15653655,
240240.30545617, 2580.00271199, 6890.73630547],
[ 6094.10132617, 5846.61932559, 2294.80686596,
2580.00271199, 240240.30545617, 61343.71356863],
[ 1985.91135194, 2152.90241365, 7166.863992 ,
6890.73630547, 61343.71356863, 240240.30545617]])
betaHH=np.array([[1.57079633, 2.42558372, 1.29852807, 1.13067005, 2.41964498, 2.4303553 ],
[0.71600894, 1.57079633, 1.05488134, 0.9288108 , 1.97712181, 2.13051745],
[1.84306458, 2.08671132, 1.57079633, 0.71601651, 0.67347314, 0.68760657],
[2.0109226 , 2.21278185, 2.42557615, 1.57079633, 0.98826407, 1.16112572],
[0.72194768, 1.16447084, 2.46811952, 2.15332858, 1.57079633, 2.42864234],
[0.71123735, 1.01107521, 2.45398609, 1.98046694, 0.71295032, 1.57079633]])
gammaHH=np.array([[ 0.00000000e+00, -1.04923238e+00, 1.05757029e+00,
8.88208378e-01, 1.51992907e+00, 1.40024175e+00],
[ 2.09236028e+00, 0.00000000e+00, -1.14726745e+00,
-9.56226609e-01, 1.69785967e+00, 1.56297278e+00],
[-2.08402236e+00, 1.99432521e+00, 0.00000000e+00,
-2.04361472e-03, -2.43231532e+00, -2.64270770e+00],
[-2.25338428e+00, 2.18536604e+00, 3.13954904e+00,
0.00000000e+00, -2.61192428e+00, -2.80947505e+00],
[-1.62166358e+00, -1.44373298e+00, 7.09277331e-01,
5.29668373e-01, 0.00000000e+00, 1.13672151e+00],
[-1.74135091e+00, -1.57861987e+00, 4.98884952e-01,
3.32117606e-01, -2.00487114e+00, 0.00000000e+00]])
# 13C CSA
deltaCSA=15.983465288047174
etaCSA=-0.10233422812456781
alphaCSA=-1.1674898472001762
betaCSA=0.914512792179852
gammaCSA=-1.312316331380307
# 1H CS/CSA
HCS=np.array([22.99922011, 24.97644825, 24.97644846, 22.99921996, 24.52192647, 23.98644806])
deltaHCSA=np.array([17.60332199, 15.80323671, 15.97227992, 18.56681946, 16.48042676, 16.77075626])
etaHCSA=np.array([-0.10418638, -0.10503486, -0.08225994, -0.14162113, -0.18843222, -0.11487855])
alphaHCSA=np.array([-2.12485296, -2.14137643, 0.91297352, -0.55202972, 2.27784746, -0.91270437])
betaHCSA=np.array([0.93737428, 2.23403156, 2.228757 , 2.17804567, 2.26820148, 0.96358604])
gammaHCSA=np.array([ 1.25827576, -0.2144375 , -2.31668105, 2.28178711, 0.17926152, -1.23977268])
ex=sl.ExpSys(v0H=400,Nucs=['13C',*['1H' for _ in range(n)]],vr=5000,pwdavg=sl.PowderAvg(q=2))
ex.set_inter('CSA',i=0,delta=deltaCSA,eta=etaCSA,euler=[alphaCSA,betaCSA,gammaCSA])
for k in range(n):
ex.set_inter('dipole',i0=0,i1=k+1,delta=delta[k],euler=[0,beta[k],gamma[k]])
ex.set_inter('CSA',i=k+1,delta=deltaHCSA[k],euler=[alphaHCSA[k],betaHCSA[k],gammaHCSA[k]])
ex.set_inter('CS',i=k+1,ppm=HCS[k])
for m in range(k+1,n):
ex.set_inter('dipole',i0=k+1,i1=m+1,delta=deltaHH[k,m],euler=[0,betaHH[k,m],gammaHH[k,m]])
L=ex.Liouvillian()
L.add_SpinEx(i=[1,2],tc=1e-4)
if n>3:
L.add_SpinEx(i=[3,4],tc=1e-4)
print(f'{(time()-t0):.1f}')
for i in range(n):
L.add_relax(Type='SpinDiffusion',i=i+1,k=0)
print(f'{(time()-t0):.1f}')
seq=L.Sequence().add_channel('13C',v1=22000)
rho=sl.Rho(rho0='13Cx',detect='13Cx')
rho,seq=rho.ReducedSetup(seq)
rho.DetProp(seq,n=500)
print(f'{"Parallel" if parallel else "Series"} time: {(time()-t0):.1f} s')
print(f'Propagators calculated: {rho.L._PropCache.cache_count[0]}, Propagators from cache: {rho.L._PropCache.cache_count[1]}')
rho.L._PropCache.cache_count[:]=0
t0=time()
rho.DetProp(seq,n=500)
print(f'{"Parallel" if parallel else "Series"} time after caching: {(time()-t0):.1f} s')
print(f'Propagators calculated: {rho.L._PropCache.cache_count[0]}, Propagators from cache: {rho.L._PropCache.cache_count[1]}')
0.1
0.1
State-space reduction: 256->80
Series time: 5.0 s
Propagators calculated: 4900, Propagators from cache: 0
Series time after caching: 0.9 s
Propagators calculated: 0, Propagators from cache: 4900
0.1
0.1
State-space reduction: 256->80
Parallel time: 5.3 s
Propagators calculated: 4779, Propagators from cache: 0
Parallel time after caching: 1.3 s
Propagators calculated: 0, Propagators from cache: 4273
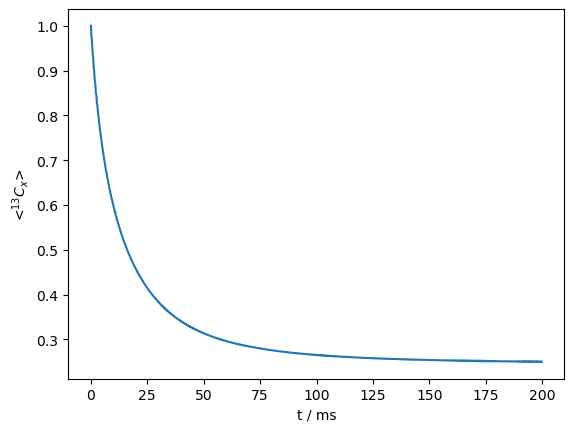
rho.plot()
<Axes: xlabel='t / ms', ylabel='<$^{13}C_x$>'>